Введение
Функция обратной пропорциональности задаётся уравнением $$f(x) = \frac{k}{x},$$ а её графиком является гипербола (нет, не та, что в литературе любит всё преувеличивать).

Теория
Что важно знать про гиперболу для экзамена:
- k — коэффициент обратной пропорциональности, отвечающий за расположение ветвей гиперболы.
Если k > 0, то ветви находятся в первой и третьей координатных четвертях.
Если k < 0, то ветви — во второй и четвёртой координатных четвертях.
- Из-за знаменателя D(y): (-∞;0)(0;+∞) и появляется асимптота — прямая, к которой гипербола приближается, но никогда не сможет её достичь и пересечь. Причём асимптоты могут быть как горизонтальными (x = 0), так и вертикальными (y = 0). У графика функции $$f(x) = \frac{k}{x},$$ асимптоты — оси координат.
- Если график смещается, то смещаются и асимптоты. Смещение происходит параллельно осям координат (то есть исходным асимптотам). В самом уравнении это отображается с помощью новых коэффициентов $$f(x) = \frac{k}{x + a} + b.$$
a — вертикальная асимптота, которая отвечает за смещение графика влево / вправо (изменение вдоль оси абсцисс, при котором добавляется число непосредственно к x).
b — горизонтальная асимптота, которая отвечает за смещение графика вверх / вниз (аналогично коэффициенту «без x» в линейной и квадратичной функции; изменение вдоль оси ординат, при котором добавляется число непосредственно к исходной f(x) = y).
Примеры заданий
Пример 1: На рисунке изображён график функции $$f(x)=\frac{k}{x}.$$ Найти $$f(0,5).$$
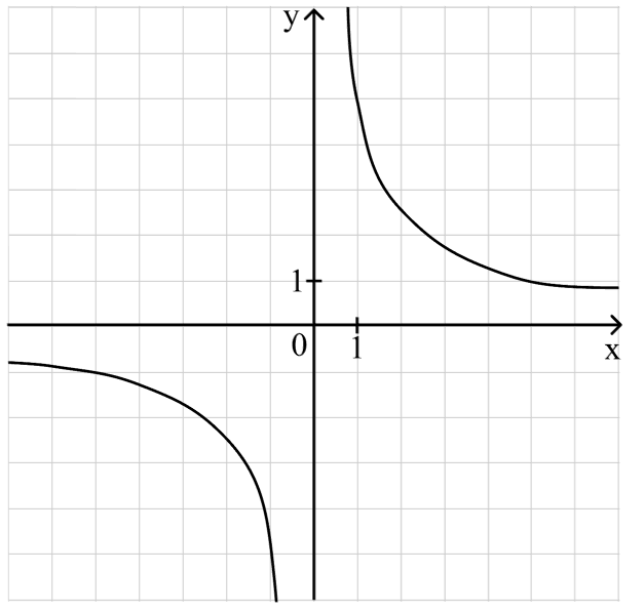
Восстановим уравнение гиперболы с помощью точки, например, с координатами (1;5)
$$5=\frac{k}{1}⇒k=5$$
$$f(0,5) = \frac{5}{0,5} = 10.$$
Проверяем: коэффициент положительный, ветви в 1 и 3 четвертях (похоже на правду).
Ответ: 10.
Пример 2: На рисунке изображены графики функций
\(f(x) = \frac{k}{x}\)
и
\(g(x) = ax+b,\)
которые пересекаются в точках A и B. Найти абсциссу точки B.
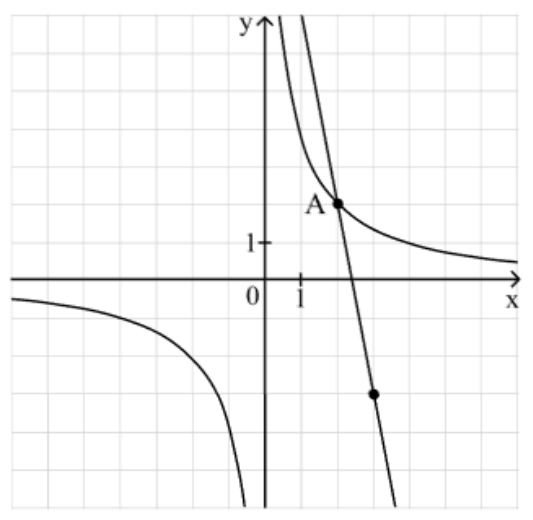
Восстановим уравнения прямой и гиперболы:
\(f(x) = \frac{k}{x}:\) A(2;2)
\(2 = \frac{k}{2}\)
k = 4
\(g(x) = ax+b:\) A(2;2)
a = -5 (через тангенс угла наклона)
\(2 = -10+b\)
b = 12
Приравняем уравнения графиков функций:
\(\frac{4}{x} = -5x+12\)
\((5x-2)(x-2) = 0\)
x = 2 или x = 0,4
Абсцисса точки B равна x = 0,4.
Ответ: 0,4.
Пример 3: На рисунке изображён график функции $$f(x) = \frac{k}{x + a}.$$ Найти $$f(-2,5).$$
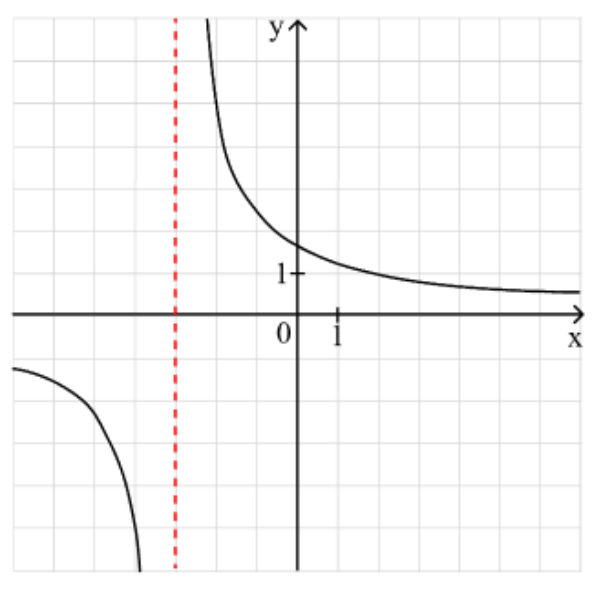
Вот эта красавица — вертикальная асимптота!
Смотри: график сместился влево, произошло изменение вдоль оси абсцисс, а это значит, что число добавили непосредственно к x. Поэтому значение a = 3 — противоположному значению по x для асимптоты.
Восстановим уравнение гиперболы с помощью точки, например, с координатами (1;2):
$$1 = \frac{k}{2 + 3} \Rightarrow k = 5.$$
$$f(-2,5) = \frac{5}{-2,5 + 3} = 10.$$
Ответ: 10.
Пример 4: На рисунке изображён график функции $$f(x) = \frac{k}{x} + b.$$ Найти, при каком значении x значение функции равно -4,8.
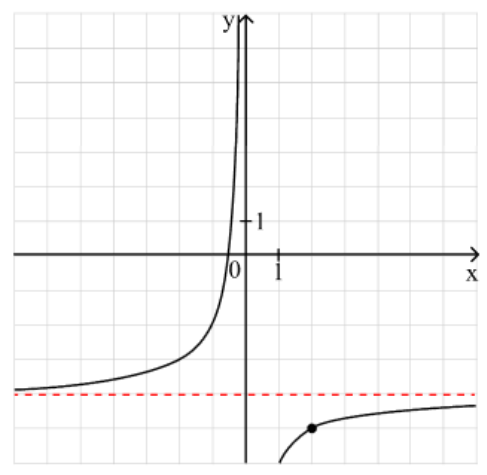
Вот и сестричка — не менее прекрасная горизонтальная асимптота!
Смотри: график сместился вниз, произошло изменение вдоль оси ординат, а это значит, что добавили число непосредственно к изначальной функции. Поэтому значение b = -4 — значению по y для асимптоты.
Восстановим уравнение гиперболы с помощью точки, например, с координатами (2; -5):
$$-5 = \frac{k}{2} — 4 \Rightarrow k = -2.$$
Проверяем: коэффициент отрицательный, ветви во 2 и 4 четвертях, что и видим на графике.
$$-4,8 = \frac{-2}{x} — 4 \Rightarrow x = 2,5.$$
Ответ: 2,5.