Введение
Есть такая функция — степенная. Общий вид уравнения $f(x) = x^n$. А дальше от значения n уже каждая из них становится по-своему интересной и уникальной. Самые известные представители этого семейства:$$ f(x) = x^2, \ f(x) = x^3, \ f(x) = x^{1/2} = c$$
Давай рассмотрим на примере функции корень, ведь он тоже может попасться на экзамене, и вспомним важное понятие области определения функции.
Область определения функции
Оказывается, бывают такие функции, в которые нельзя подставлять совсем уж всё, что захочется. У них существуют ограничения, из-за которых формируется область, где она вообще существует, то есть область определения функции. Здесь речь идёт про «x», а точнее про то, какие именно значения можно подставлять.
Обозначение: D(y).
Есть ещё понятие множества значений функции, но здесь само название говорит за себя: это значения, которые может принимать y на её области определения.
На примере $y = x^{1/2} = \sqrt{x}$ мы понимаем, что $D(y): x \ge 0$.
Примеры заданий
Пример 1. На рисунке изображён график функции $f(x) = k\sqrt{x}$. Найти f(100).
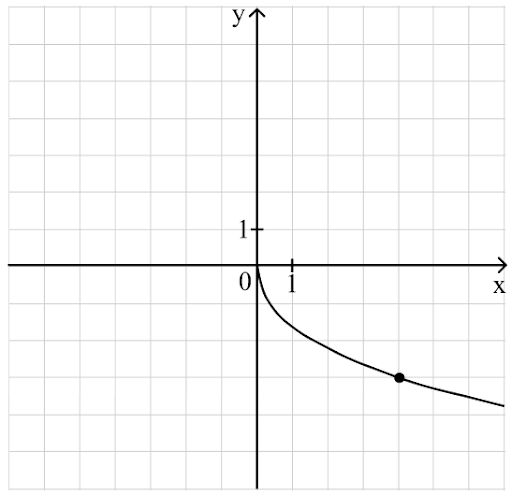
Возьмём точку (4; -3) и подставим в уравнение:
$-3 = k\sqrt{4}$
$k = -1,5$
$f(100) = -1,5\sqrt{100} = -15.$
Ответ: -15.
Пример 2. На рисунке изображён график функции $f(x) = k\sqrt{x}$. Найти значение x, при котором f(x) = -6,5.
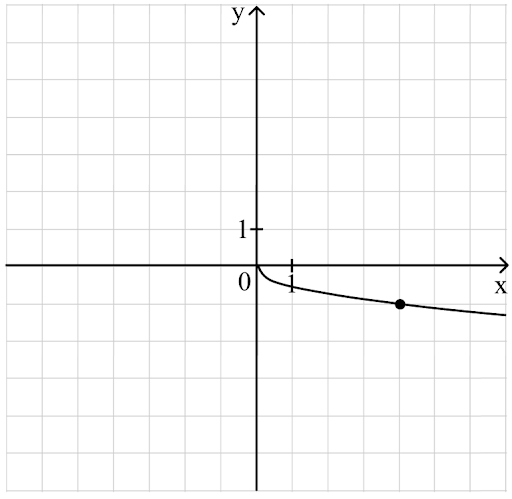
Возьмём точку (4;–1) и подставим в уравнение:
$-1 = k\sqrt{4}$
$k = -\frac{1}{2}$
$-6,5 = -\frac{1}{2}\sqrt{x}$
$x = 169$
Ответ: 169.
